1. Классическая механика и границы ее применимости.

 

Раньше других разделов физики стала развиваться механика. Механика есть наука о движении и равновесии тел. В широком смысле слова движение материи есть всякое ее изменение. Однако в механике под движением понимается только простейшая его форма, а именно перемещение тела относительно других тел. Принципы механики были впервые сформулированы Ньютоном (1643–1727 гг.) в его основном труде «Математические начала натуральной философии» (1687 г.).

 

После Ньютона механика начала быстро развиваться, однако до начала XX  века это развитие шло в основном в направлении совершенствования математических методов механики и применения ее законов ко все новым и новым областям знания. Несомненные в то время успехи механики привели к представлению, что законов механики достаточно для объяснения всех явлений природы (механистический взгляд на природу вещей).

 

Положение в корне изменилось с открытием электрических и магнитных явлений, особенно с открытием электромагнитных волн. И их, конечно, пытались объяснить механистически, как волны в некоторой пронизывающей все пространство среде, называемой эфиром (как волны на поверхности воды или звук в воздухе). Однако эти попытки не увенчались успехом.

 

Окончательный отказ от механистических представлений произошел в начале XX века. Первое, что выяснилось, — это то, что механика Ньютона применима лишь к сравнительно медленным движениям со скоростями, заметно меньшими скорости света в вакууме   км/с. Движения, скорости которых приближаются к скорости света, называют релятивистскими. Но скорость света огромна. В повседневной жизни мы имеем дело со скоростями, заметно меньшими. Так, скорость реактивного самолета может в 2–3 раза (обычно не больше) превысить скорость звука в воздухе,   м/с = 0,3 км/с 1. Скорость спутника или космического корабля порядка 10 км/с. Такого же порядка скорость движения Земли по орбите вокруг Солнца (30 км/с). Наконец, скорость движения Солнца по своей орбите вокруг центра нашей Галактики (кстати, ее называют Млечным путем) порядка 300 км/с, что меньше скорости света в 1000 раз.

 

Второе ограничение классической механики заключается в ее неприменимости к описанию явлений микромира, то есть к движениям тел малой массы в малых участках пространства. Более общей наукой, описывающей такие движения, является квантовая механика, согласно которой неопределенность в знании значений координат и импульса определяется соотношением неопределенности Гейзенберга

 

 (1)    

 

В применении к обычным телам, например к футбольному мячу весом 0,5 кг, движущемуся со скоростью 30 м/сек, с хорошей точностью применима механика классическая. Так, если мы не знаем скорость с точностью выше, чем   мкм/с (то есть  — огромная точность), а   мкм (10 Å), то   эрг·сек   эрг·сек. Таким образом, классическая механика Ньютона изучает медленные движения макроскопических тел.

 

2) Системы отсчета. Основные кинематические параметры: траектория, путь, перемещение, скорость, ускорение. Прямолинейное движение. Тангенциальное и нормальное ускорение

система отсчета - система координат ,тело отсчета и способ измерения времени

Траекторией тела называется линия, описываемая в пространстве движущейся материальной точкой. Путь – длина участка траектории от начального до конечного перемещения материальной точки. Радиус-вектор   – вектор, соединяющий начало координат и точку пространства. Перемещение – вектор  , соединяющий начальную и конечную точки участка траектории, пройденные за время. Скорость – физическая величина, характеризующая быстроту и направление движения в данный момент времени. Средняя скорость определяется как  . Средняя путевая скорость равна отношению пути, пройденному телом за промежуток времени к этому промежутку.  .   ускорение – изменение скорости за время (dV/dt) или 2-я производная координаты по времени (a=d^2x/d^2t)

 

Прямолинейное движение (a=0): x=x₀+V₀t  Равнопеременное движение(а=const): x=x₀+V₀t+at²/2

Вращательное движение – если траектория окружность.Положение тела можно определять углом поворота радиус-вектора, при котором

угол берется от заранее выбранного направления. R=r(t)=const Закон движения в угловой форме: φ=φ(t).Угловая скорость – вектор напра-

вленный вдоль оси вращения, направление определяется по правилу левой руки.Вектор углового ускорения совпадает с вектором угловой

скорости при ускоренном движении и направлен в противоположную сторону при замедленном.

ω = dφ/dt – угловая скорость  V=dS/dt=Rdφ/dt=Rω   аt= dV/dt=Rdω/dt=Rε     ω=2pn              ω=ω₀ ± εt

ε =dω/dt - угловое ускорение  l=S=Rφ   T=2p/ω        а_н=V²/R=Rω²                            n=1/T=ω/2p     ω=ω₀t ± εt²/2

 

Быстрота изменения скорости определяется ускорением a_cp =DV/Dt Ускорение тела это первая производная скорости по времени.

a_cp=DV/dt           a=d/dt(d/dt)r=d²r/dt²

Вектор ускорения можно разложить на 2 составляющие:

аt - тангенциальное (направленное по касательной) и а_н – нормальное

(направлено в сторону противоположную нормали к траектории).

а= аt+ а_н                аt=d²s/dt²          а= √аt² +а_н²   a_н=V²/R           R –радиус кривизны траектории в данной точке

Ускорение характеризует быстроту изменения модуля вектора скорости.Вектор ускорения можно разложить по координатам:

a=a_xi+a_yj              а= √а_x² +а_y²

 

 

3) Кинематика вращательного движения. Основные параметры: угловое перемещение, угловая скорость, угловое ускорение. Связь угловых и линейных параметров.

Кинематические характеристики: линейная и угловая скорости и ускорения, связь между ними.

Угловой скоростью вращения твердого тела называется вектор w, численно равный первой производной от угла поворота по времени,

 

w = df/dt

 

и направленный вдоль оси вращения таким образом, чтобы из его конца вращение тела было видно происходящим против часовой стрелки. Направление вектора w совпадает с направлением поступательного движения буравчика, рукоятка которого вращается вместе с телом.

 

Линейная скорость v произвольной точки М вращающегося тела определяется как векторное произведение по формуле Эйлера

 

v = [wr]

 

где r - радиус-вектор, проведенный в точку М из произвольной точки О оси вращения тела. Численное значение v линейной скорости точки М прямо пропорционально ее расстоянию R от оси вращения:

 

v = wr sina = wR

 

где a - угол между векторами w и r.

 

Угловым ускорением изменения во времени вектора угловой скорости тела. При вращении вокруг неподвижной оси направление вектора w сохраняется и

 

e = dw/dt = d2f/dt2

 

причем вектор e совпадает но направлению с w в случае ускоренного вращения (e > 0) и противоположен ему по направлению в случае замедленного вращения (e < 0)

Линейное ускорение произвольной точки М (r) вращающегося тела равно

 

a = dv/dt = d/dt | wr | = | er | + | w | wr ||

 

4) Динамика поступательного движения. Основные динамические параметры: масса, импульс тела, сила, виды сил. Силы в механике: сила тяготения, сила трения, сила упругости. Законы Ньютона.

Поступательным называется такое движение абсолютно твердого тела, при котором любая прямая, жестко связанная с телом, перемещается параллельно самой себе. Все точки тела, движущегося поступательно, в каждый момент времени имеют одинаковые скорости и ускорения, а их траектории полностью совмещаются при параллельном переносе. Поэтому кинематическое рассмотрение поступательного движения абсолютно твердого тела сводится к изучению движения любой его точки. В самом общем случае поступательно движущееся твердое тело обладает тремя степенями свободы.

 

Количественной мерой инертности является масса тела. Отношение масс взаимодействующих тел равно обратному отношению модулей ускорений. Второй закон Ньютона устанавливает связь между кинематической характеристикой движения – ускорением, и динамическими характеристиками взаимодействия – силами.  , или, в более точном виде,  , т.е. скорость изменения импульса материальной точки равна действующей на него силе. При одновременном действии на одно тело нескольких сил тело движется с ускорением, являющимся векторной суммой ускорений, которые возникли бы при воздействии каждой из этих сил в отдельности.

По второму закону Ньютона независимо от того, находилось ли тело в покое или двигалось, изменение его скорости может происходить только при взаимодействии с другими телам. Если на тело массой m в течение времени t действует сила F и скорость его движения изменяется от V0 доV, то ускорение тела равно  . На основании второго закона Ньютона для силы F можно записать   _=> . Физическая величина, равная произведению силы на время ее действия, называется импульсом силы.

 

Из того, что тела независимо от своей массы падают с одинаковым ускорением, следует, что сила, действующая на них, пропорциональна массе тела. Эта сила притяжения, действующая на все тела со стороны Земли, называется силой тяжести. Сила тяжести действует на любом расстоянии между телами.

Сила, возникающая на границе взаимодействия тел при отсутствии относительного движения тел, называется силой трения покоя. Сила трения покоя равна по модулю внешней силе, направленной по касательной к поверхности соприкосновения тел и противоположна ей по направлению.

Сила, возникающая в результате деформации тела и направленная в сторону, противоположную перемещениям частиц тела при этой деформации, называется силой упругости.

 

Третий закон Ньютона.

При любом взаимодействии двух тел отношение модулей приобретенных ускорений постоянно и равно обратному отношению масс. Т.к. при взаимодействии тел векторы ускорений имеют противоположное направление, можно записать, что  . По второму закону Ньютона сила, действующая на первое тело равна, а на второе. Таким образом, . Третий закон Ньютона связывает между собой силы, с которыми тела действуют друг на друга. Если два тела взаимодействуют друг с другом, то силы, возникающие между ними приложены к разным телам, равны по величине, противоположны по направлению, действуют вдоль одной прямой, имеют одну и ту же природу.

  Второй закон Ньютона устанавливает связь между кинематической характеристикой движения – ускорением, и динамическими характеристиками взаимодействия – силами., или, в более точном виде,  , т.е. скорость изменения импульса материальной точки равна действующей на него силе.

Первый закон Ньютона, он же закон инерции, гласит: “существуют такие системы отсчета, относительно которых поступательно движущиеся тела сохраняют свою скорость постоянной, если на них не действуют другие тела”.

 

5) Инерциальные системы отсчета. Силы инерций. Центробежная сила. Сала Кориолиса.

Системы отсчета, относительно которых тела при отсутствии внешних воздействий движутся прямолинейно и равномерно, называются инерциальными системами отсчета. Системы отсчета, связанные с землей считают инерциальными, при условии пренебрежения вращением земли.

 

Силы инерций появляются при прямолинейном, равномерном движений.

 k) ma=mg+T

                                                  k1) ma1=mg+T+Fи

                                                    ma1=0 => Fи=-ma

Центробежная сила появляется когда тело покоется во вращательной системе отсчета.

ω - константа

Fи=Fцентрострем

K – внешняя система отсчета

K1 – система отсчета во вращательной системе.

k) ma=T+mg= Fцентрострем

k1) ma=T+mg+ Fи=0 => Fи=-Fцентрострем=-ma => Fцентробеж=Fцентрострем

 

Сила Кориолиса появляется при движение тела поступательно во вращательной системе отсчета

ω – константа

Fи=Fупр

Fи=Fкр=2m[Vω]

В результате действия силы Кориолиса молекулы воды будут размывать восточный берег реки текущей на север относительно течению реки.

 

6) Центр инерций. Движение центра инерций. Замкнутые системы отчета. Закон сохранения импульса и условия его выполнения. Реактивное движение. Движение тела переменной массы. Уравнение Мещерского и Циолковского.

Вектор импульса системы точкой приложенной имеет так называемый центр масс. В произвольной системе отсчета центр масс данной системы задается радиус вектором определенным следующим образом:

 ri - радиус вектор I – й материальной точки.

Продифференцируем левую и правую часть равенства по времени

|

Точка с координатами R_c называется центром инерции (или центром масс) системы из двух материальных точек. Из уравнения (14) следует, что, каким бы сложным ни казалось движение каждой из масс, пpоизводная dR_c /dt = const. Таким обpазом, центр инерции движется с постоянной скоростью (независимо от наличия колебательного и вращательного движения системы). Обозначим эту скорость как V_c:

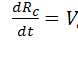
Подставляя сюда выражение для R_c и дифференцируя, получаем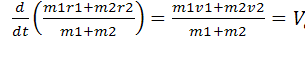

Эта формула определяет скорость центра инерции V_c через массы и скорости составляющих систему частиц. К движению именно этой точки относится первый закон Ньютона, и скорость этой точки надо считать скоростью движения системы как целого ¹. Если мы согласимся на такое определение скорости движения системы как целого, то тогда импульс системы как целого должен быть равен произведению суммарной массы системы m₁ + m₂ на ее скорость V_c, то есть (m₁+m₂)V_c. С другой стороны,

  Импульс в замкнутых системах отсчетов остаются неизменными.

Импульс тела. Закон сохранения импульса. Реактивное движе­ние.

По второму закону Ньютона независимо от того, находилось ли тело в покое или двигалось, изменение его скорости может происходить только при взаимодействии с другими телам. Если на тело массой m в течение времени t действует сила F и скорость его движения изменяется от V0 до V, то ускорение тела равно  . На основании второго закона Ньютона для силы F можно записать   _=>  . Физическая величина, равная произведению силы на время ее действия, называется импульсом силы. Импульс силы показывает, что существует величина, одинаково изменяющаяся у всех тел под воздействием одинаковых сил, если время действия силы одинаково. Эта величина, равная произведению массы тела на скорость его движения, называется импульсом тела. Изменение импульса тела равно импульсу силы, вызвавшей это изменение. Возьмем два тела, массами m1 и m2, движущиеся со скоростями V1и V2. По третьему закону Ньютона силы, действующие на тела при их взаимодействии, равны по модулю и противоположны по направлению, т.е. их можно обозначить как F и -F . Для изменений импульсов при взаимодействии можно записать  . Из этих выражений получим, что , то есть векторная сумма импульсов двух тел до взаимодействия равна векторной сумме импульсов после взаимодействия. В более общем виде закон сохранения импульса звучит так: Если , то

Внекоторых случаях масса движущегося тела изменяется в результатах непрерывного отсоединения или присоединения небольших порций масс. Примером является реактивное движение.

 - изменение массы ракеты со временим

  - уравнение Мещерского, позволяет найти скорость ракеты в произвольный момент времени.  - формула Циолковского , скор. Ракеты в произвол. Мом. Времени.

 - реактивная сила, обозн ее-  

| - мин. Означ. Что сила напра. В прот. Стор.от истеч. Газов.

 

7) Динамика вращательного движения материальной точки. Основные параметры: момент силы, момент импульса, момент инерций. Основной закон динамики вращательного движения.

а) Пусть материальная точка массы m вращается относительно оси ОО΄. Обозначим r - радиус-вектор, проведенный от оси вращения до  точки приложения силы F (Рисунок 10).

 

 

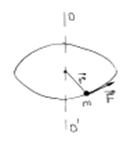
Рисунок 10.Вращение материальной точки

Моментом силы F относительно оси вращения называется вектор M, равный векторному произведению радиус-вектора на вектор силы M = [r∙F] и  направленный по оси вращения в сторону, определяемую по правилу правого буравчика

Модуль вектора момента силы равен M = F∙r∙sinα, где α - угол между векторами r и F.

 

Момент инерции.

При изучении вращения твердого тела пользуются понятием момента инерции. Моментом инерции системы (тела) относительно оси вращения называется физическая величина, равная сумме произведений масс n материальных точек системы на квадраты их расстояний до рассматриваемой оси:

 

В случае непрерывного распределения масс эта сумма сводится к интегралу

 

где интегрирование производится по всему объему тела.

Величина r в этом случае есть функция положения точки с координатами x,y,z

Количеством движения (импульсом) материальной точки называется вектор К, равный произведению массы m точки на ее скорость v:

K = mv

Количеством движения системы k материальных точек называется вектор К, равный геометрической сумме количеств движения всех точек системы:

K= SKi = Smivi

Количество движения системы материальных точен равно произведению массы m всей системы на скорость ее центра инерции:

K=mVc.

Скорость Vc представляет собой скорость поступательного движения системы.

Произведение модуля силы, вращающей тело, на ее плечо называется моментом силы.

M=F*l

 Единицей измерения момента силы является 1 ньютон*метр.

       Отсюда можно сформулировать еще одно правило равновесия рычага:

    рычаг находится в равновесии под действием двух сил, если момент силы, вращающей его по часовой стрелке, равен моменту силы, вращающей его против часовой стрелки.

 

M=Iε – основное уравнение динамики вращательного движения. L=Iω –вращательный импульс

Момент равный сумме моментов сил приложенных к телу – главный момент системы.M₀=∑M_i направление определяется по п. правой руки.

dL/dt=M₀ –основное уравнение динамики при вращении

 

8) Момент инерций твердого тела. Теорема Штейнера. Расчет момента инерций стержня, диска. Основной закон динамики вращательного движения твердого тела. Твердое тело.

Теорема Штейнера: момент инерции тела I относительно любой оси вращения равен моменту его инерции Ic относительно параллель-

ной оси,проходящей через центр масс С тела, сложенному с произведением массы m тела на квадрат расстояния D между осями.

Момент инерции тела относительно оси вращения – это физическая величина, равная сумме произведений масс n материальных точек

Системы на квадраты их расстояний до рассматриваемой оси.Момент инерции зависит от: геом. формы телаи положения оси вращения.

I=∑m_ir_i²  I=mr² - мат.точка  I=Mr² – кольцо I=ml²/12 –стержень(ось через центр) I=ml²/3 -стержень(ось через конец) I=2mR²/5 –шар

I=mR²/2 –диск или цилиндр       I=1,5mR² – диск (ось через край)  dA=Mdφ    A=∫Mdφ – работа при вращательном движении.

 

Момент инерций твердого тела. Момент инерций физическая величина характеризует инертное тела, т.е. способность тела сопротевляца изменению состояния покоя или равномерного вращения. Момент инерций определяется как:  - применяется при дескретном распределение массы   Оба выражения определяет момент инерций относ. Собст. Оси проход. Через центральную ось. Момент инерций относительно произвольной оси определяется по теореме Штеинера 

Твердое тело – это тело расстояние между 2-мя любыми точками которого остается неизменным при любых взаимодействиях этих точек.

 

10) Закон сохранения импульса.

1. Совокупность тел, частиц (например, в газе) или отдельное твердое можно рассматривать как систему материальных точек. Если система с течением времени изменяется, то  это означает, что изменяется ее состояние. Зная законы действующих на частицы системы сил и состояние системы в начальный момент времени, можно с помощью уравнений движения рассчитать состояние системы в любой момент времени.  Но в некоторых случаях это может быть задачей достаточно сложной (сложна сама система или неизвестны законы действующих сил, или детальное рассмотрение поведения отдельных частиц системы не имеет смысла, например, в газе).

Возникает вопрос:  нет ли каких-либо общих принципов, которые позволили бы иначе подойти к решению задач и обойти возникшие трудности? Оказалось, такие принципы есть. Это законы сохранения  энергии,  импульса  и  момента  импульса  (см. [7], стр. 52-57).

Эти законы справедливы не только в рамках классической механики. Все они являются универсальными законами природы, выполняются и в макромире, и в микромире, и во всей Вселенной. В настоящее время неизвестно ни одного эксперимента и ни одного физического явления, в котором упомянутые универсальные законы сохранения нарушались бы.

Закон сохранения импульса выполняется для замкнутых систем (см. §2.2.1 п.1).

2.Справедливость закона сохранения импульса можно показать для замкнутой системы, состоящей из  двух тел, применяя второй и  третий законы Ньютона. Пусть первое тело, имеющее массу m₁, движется со скоростью V1, второе тело, масса которого m_2, движется со скоростьюV_2.

При столкновении тела взаимодействуют друг с другом, и, согласно Третьему закону Ньютона, сила F₁₂ =-F_{21 ,}  по второму закону Ньютона сила F_12,  действующая на первое тело, изменит импульс первого тела, можно записать , точно так же можно записать, что сила F₂₁ изменит импульс второго тела: . Подставим значения F₁₂  и F₂₁ в третий закон Ньютона: , т.к.  время взаимодействия  -  одно и то же, то:   или .

Рассматриваемая нами замкнутая система состояла из двух тел, полный вектор импульса этой системы

- это изменение вектора полного импульса. При взаимодействии двух тел получили, что изменение вектора полного импульса  , следовательно, полный вектор импульса системы при взаимодействии не изменился: если , то P  = const.

Если система состоит из N тел, то P = m₁∙v₁ + m₂∙v₂ + ........+ m_N∙v_N есть полный вектор импульса замкнутой системы, и  P  = const.

Закон сохранения импульса  (ЗСИ).

Полный вектор импульса замкнутой системы есть величина постоянная при любых взаимодействиях внутри данной системы. Только внешние силы изменяют импульс системы.

3. Если векторная сумма внешних сил  не равна нулю, то надо посмотреть, нет ли такого направления, вдоль которого внешние силы не действуют или сумма их проекций на это направление равна нулю. Если такое направление в движении тел, входящих в систему, есть, то можно применять закон сохранения для проекции полного вектора импульса системы на выделенное направление.

 

11) Энергия. Виды энергий. Механическая энергия. Кинетическая энергия при поступательном и вращательном движение.

Энергия.

1. Наиболее общим определением понятия энергии можно считать то, которое связано с понятием состояния системы (или тела). Энергия всегда является функцией состояния системы (тела). В любом состоянии система имеет определенное значение энергии и может сохранять это состояние, а значит и энергию этого состояния, сколь угодно долго. Для перехода системы (тела) в другое состояние должна быть совершена работа.

Физическая величина, характеризующая способность тела или системы тел совершить работу, называется энергией.

Состояние системы (тела) может меняться в процессе движений. Формы движений в природе  различны. Для количественного сравнения разных форм движений  и служит понятие энергии. Поэтому можно дать другое определение для энергии.

Энергией  называется   физическая величина, являющаяся общей мерой различных форм движения материи.

Различают виды энергии  механическую, внутреннюю, электромагнитную, химическую, ядерную и т.д.

Механическая энергия может быть обусловлена или движением тела с некоторой скоростью (кинетическая энергия), или расположением данного тела в системе других тел определенной конфигурации  (потенциальная энергия)  W_мех. = W_кин. + W_пот..

Кинетическая энергия.

1. Кинетической энергией тела называется энергия его механического движения.

Изменение  кинетической  энергии тела  под действием силы равно работе этой силы. 

Физическая величина    называется кинетической энергией, а величина  , равная  разности кинетических энергий конечного состояния системы (индекс 2) и начального состояния (индекс 1), называется  приращанием  кинетической энергии.

Если на тело действуют несколько сил, и каждая из них совершает работу, и в результате этого меняется кинетическая энергия тела, то полная работа равна алгебраической сумме работ всех сил, действующих на тело. Энергия тела меняется за счет совершения работы.

Итак, связь работы и кинетической энергии  задается  соотношением:

А_{всех сил} = ∆W_кин = (W_кин)_кон. - (W_кин.)_нач.,

т.е. работа всех сил равна изменению кинетической энергии тела (или системы).

Работа - мера изменения энергии (физический смысл работы).

2. Кинетическая энергия вращающегося тела.

Твердое тело вращается вокруг неподвижной оси. Полная кинетическая энергия вращающегося тела равна:

 

где I - момент инерции тела относительно оси вращения.

Потенциальная энергия.

1. Потенциальная энергия - энергия, определяемая взаимным расположением тел или отдельных частей тела относительно друг друга.

Когда меняется конфигурация системы тел или частиц одного тела относительно друг друга, должна совершаться работа.

Пространство, в каждой точке которого на тело действует определенная сила, называется физическим или силовым полем.

Поэтому когда тело перемещается вблизи Земли, то говорят, что тело двигается в силовом поле тяготения Земли или в потенциальном поле Земли. Потенциальная энергия тяготения равна (W_пот)_тяг. = mgh,

h - расстояние между телом и Землей.

В растянутой (или сжатой) пружине на каждую ее точку действует сила упругости, в этом случае можно говорить о потенциальном поле упругости. Потенциальная энергия упругости равна (W_пот)_упр. = (kl²)/2, l - длина растянутой пружины, отсчет х от положения равновесия.

При делении сил, действующих на тело, на внешние и внутренние  рассмотренные в примерах сила тяготения  (в системе "тело - Земля") и сила упругости растянутой (сжатой) пружины можно отнести к внутренним силам. Поэтому верно утверждение, что каждой конфигурации произвольной системы частиц присуща своя собственная потенциальная энергия, и работа всех внутренних потенциальных сил, приводящая к изменению этой конфигурации, равна взятому со знаком минус приращению (убыли) потенциальной энергии системы.

В физике работа неразрывно связана с изменением состояния тела или системы. Это изменение может выражаться самым различным образом: а) тело приобретает другую скорость, б) тело поднимается на другой уровень, в) тело деформируется, г) тело заряжается, д) тела намагничивается и т.д. Состояние механической системы (или тела) характеризуется одновременным заданием координат и скоростей всех точек системы (или тела) и может изменяться в процессе движения.

Процесс изменения характера движения тела происходит при его силовом взаимодействии с другими телами. Для количественного описания процесса  вводят понятия силы и работы, совершаемой силой.

1.Если на тело действует постоянная сила F  (Рисунок 13), и это приводит к перемещению ∆r тела, то элементарной работой ∆А постоянной силы называется скалярное произведение вектора силы F и вектора перемещения ∆r:

∆А = (F∙∆r) =  ½F½½∆r½cos a ,

где a - угол между направлениями векторов силы F и перемещения ∆r, (F∙∆r) – скалярное произведение двух векторов (см.[8]).

Рисунок 13 - Перемещение тела под действием постоянной силы.

Работа ∆А - скаляр. Если угол a - острый, то ∆А  положительная величина, и говорят, что сила совершает работу. Если угол a - тупой, то ∆А - отрицательная  величина, и говорят, что работа совершается против действия силы. Если  a = 90⁰, т.е. направления силы и перемещения взаимно перпендикулярны, то такая сила работы не совершает ∆А = 0. Такая сила не может изменить величину скорости тела, но она меняет направление скорости.

 

12) Потенциальная энергия. Градиент потенциальной энергий. Работа диссипативных и консервативных сил.  Потенциальное поле сил. Связь силы и потенциальной энергий. Потенциальная энергия двух точечных взаимодействующих масс.

Потенциальная энергия.

1. Потенциальная энергия - энергия, определяемая взаимным расположением тел или отдельных частей тела относительно друг друга.

Когда меняется конфигурация системы тел или частиц одного тела относительно друг друга, должна совершаться работа.

Пространство, в каждой точке которого на тело действует определенная сила, называется физическим или силовым полем.

Поэтому когда тело перемещается вблизи Земли, то говорят, что тело двигается в силовом поле тяготения Земли или в потенциальном поле Земли. Потенциальная энергия тяготения равна (W_пот)_тяг. = mgh,

h - расстояние между телом и Землей.

В растянутой (или сжатой) пружине на каждую ее точку действует сила упругости, в этом случае можно говорить о потенциальном поле упругости. Потенциальная энергия упругости равна (W_пот)_упр. = (kl²)/2, l - длина растянутой пружины, отсчет х от положения равновесия.

При делении сил, действующих на тело, на внешние и внутренние  рассмотренные в примерах сила тяготения  (в системе "тело - Земля") и сила упругости растянутой (сжатой) пружины можно отнести к внутренним силам. Поэтому верно утверждение, что каждой конфигурации произвольной системы частиц присуща своя собственная потенциальная энергия, и работа всех внутренних потенциальных сил, приводящая к изменению этой конфигурации, равна взятому со знаком минус приращению (убыли) потенциальной энергии системы.

 

Градиент это вектор модуль которого равен производной по координате направле-

ния наиб. возрастания функции, и направленный в сторону возрастания функции.ЗСЭ: в замкнутой системе, где действуют только потенци-

альные силы полная механическая энергия остается постоянной.

   Работа силы тяжести (потенциальная энергия тела в поле силы тяжести)

Если тело перемещается вверх, работа силы тяжести отрицательна; вниз – положительна.

Работа силы тяжести не зависит от траектории движения тела,

 а зависит лишь от перепада высот (от изменения положения тела над поверхностью земли).

Работа силы тяжести по замкнутому контуру равна нулю.

Силы, работа которых по замкнутому контуру равна нулю, называются потенциальными (консервативными). В механике потенциальными являются сила тяжести и упругая сила (в электродинамике – сила Кулона), непотенциальными – сила трения (в электродинамике – сила Ампера, Лоренца).

Потенциальная энергия тела в поле силы тяжести:

Работа потенциальной силы всегда равна убыли потенциальной энергии:

Работа упругой силы (потенциальная энергия упруго деформированного тела)  

/* Если какая-то физическая величина изменяется по линейному закону, ее среднее значение равно полусумме начального и конечного значений – F_y */

Потенциальная энергия упруго деформированного тела:

Потенциальная энергия двух точечных взаимодействующих масс.

 

Если пренебречь всеми релятивистскими эффектами и ограничиться слабыми стационарными гравитационными полями, то общая теория относительности сводится к ньютоновской теории всемирного тяготения. В этом случае, как известно, потенциальная энергия взаимодействия двух точечных частиц с массами m1 и m2 дается соотношением , где r - расстояние между частицами, G - ньютоновская гравитационная постоянная, играющая роль константы гравитационного взаимодействия. Данное соотношение показывает, что потенциальная энергия взаимодействия V (r) отлична от нуля при любом конечном r и спадает к нулю очень медленно. По этой причине говорят, что гравитационное взаимодействие является дальнодействующим.

 

13) Закон сохранения механической энергий. Закон сохранения импульса. Понятие замкнутой консервативной системы.

Законы сохранения энергии в механике.

Потенциальная энергия характеризует взаимодействующие тела, кинетическая – движущиеся. И та, и другая возникают в результате взаимодействия тел. Если несколько тел взаимодействую между собой только силами тяготения и силами упругости, и никакие внешние силы на них не действуют (или же их равнодействующая равна нулю), то при любых взаимодействиях тел работа сил упругости или сил тяготения равна изменению потенциальной энергии, взятой с противоположным знаком. В то же время, по теореме о кинетической энергии (изменение кинетической энергии тела равно работе внешних сил)  работа тех же сил равна изменению кинетической энергии. 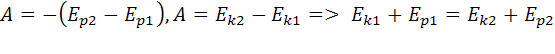  . Из этого равенства следует, что сумма кинетической и потенциальной энергий тел, составляющих замкнутую систему и взаимодействующих между собой силами тяготения и упругости, остается постоянной. Сумма кинетической и потенциальной энергий тел называется полной механической энергией. Полная механическая энергия замкнутой системы тел, взаимодействующих между собой силами тяготения и упругости, остается неизменной. Работа сил тяготения и упругости равна, с одной стороны, увеличению кинетической энергии, а с другой – уменьшению потенциальной, то есть работа равна энергии, превратившейся из одного вида в другой.

Импульс силы показывает, что существует величина, одинаково изменяющаяся у всех тел под воздействием одинаковых сил, если время действия силы одинаково. Эта величина, равная произведению массы тела на скорость его движения, называется импульсом тела. Изменение импульса тела равно импульсу силы, вызвавшей это изменение. Возьмем два тела, массами m1 и m2, движущиеся со скоростями V1и V2. По третьему закону Ньютона силы, действующие на тела при их взаимодействии, равны по модулю и противоположны по направлению, т.е. их можно обозначить как F и -F . Для изменений импульсов при взаимодействии можно записать . Из этих выражений получим, что , то есть векторная сумма импульсов двух тел до взаимодействия равна векторной сумме импульсов после взаимодействия. В более общем виде закон сохранения импульса звучит так: Если. , то

Силы действующие в потенциальных полях называются консервативными.

 

14) Принцип относительности Галилея. Преобразование Галилея. Постулаты Эйнштейна. Преобразование Лоренца. Специальная теория относительности. Релятивистская механика.

Любое тело остается неподвижным, пока на него не действуют другие тела. Тело, двигавшееся с некоторой скоростью, продолжает двигаться равномерно и прямолинейно до тех пор, пока не него не подействуют другие тела. К таким выводам о законах движения тел впервые пришел итальянский ученый Галилео Галилей.

 

Классическая механика основывается на преобразование Галилея: Все законы относительно ИСО. Рассмотрим 2 ИСО k и k1 движущиеся с постоянной скоростью относительно системы отсчета k. Соответственно в k1 задается положение этой точки задается r1 Между собой эти вектора связаны. R = r1+Ut | d/dt – преобразование координат

V = V1+ U – закон сложения скоростей Галилея. Из полученного выражения следует, что скорость является величенной относительной зависящий от выбора системы отсчета. Продифференцируем еще раз по d/dt.

Получим: a=a1   m=const => F=F1. Из полученого выражения следует что ускорение a  следовательно и F  является величиной абсолютной т.е. законы динамики инвариантны относительно системы отсчета. 

 

Постулаты Энштейна.

1) Расширенный постулат принципа относительности Галилея. Все законы (прирощения ?) инвариантности относительно инерциальных систем отсчета.

2) Скорость света в вакууме не зависит от движение источников или приемников света и один для всех инерциальных систем отсчета.

Преобразование Лоренца.

Релитивиская механика и преобразование Лоренца в частности не отвергает полностью классическую механику, а лиш ограничивает область ее применения для малых по сравнению со скоростью света скоростями.

 

СТО

Опыт Манкийсона – Моргана . Впервые основы классической физики были подвергнуты сомнениям опыт Маикийсона. Согласно волновой теорий, свет представляет собой поперечное колебание эфира распространяющиеся со временем. Эфир представлялся как абсолютно пронзающиеся тело заполняющие все пространство, но в тоже время из поперечной световой волны следует, что эфир является абсолютно твердым телом в любом случае, в соответствие с законом сложения скоростей Галилея. Скорость света должна была зависит от скорости движения источника и приемника света в опыте Маикийсон использовал скорость земли при вращение вокруг солнца (30 км/с) измерил время прохождения света одинаковое расстояние в направление движения Земли и …..

Многочисленные опыты в попытках обнаружения эфира ветра дали отрицательный результат т.е. скорость света независима от скорости источника или приемника света и были одинаковы для всех инерциальных систем отсчета. Закон сложения скоростей Галилея для света оказался не применимым

    Фактически этот опыт Эйнштейн положил в основу СТО или релитивиской механики.

 

Релятивисткой механика действует при скоростях близких к скорости света.

 

15) Лоренцево сокращение длины. Относительность пространства и времени. Правило сложение скоростей.

Длина определяется разностью двух координат в один и тотже момент времени.

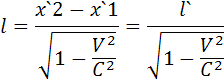
_{l`</sub>- это продольные размеры тела в системе   <sub>k`} относительно которой тело покоится. Иначе говоря собственная длина тела L.

L – длина этогоже тела в системе k относительно которой тело движется со скоростью V следовательно 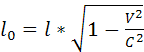  - из данного выражения следует что продольные размеры движущихся тел сокращаются ( размеры в направление движения).

 

Пусть в начальный момент времени когда начало отсчета системы совпадает в положение направления оси Х был излучин импульс света, тогда через какойто промежуток времени t положения этого импульса в системе отсчета Х будет определен как k)x а в  k1)x1     x не равен x1 x=ct   x1=c1*t1  в классической механике полагали что t=t1, а т.к. х не равен  х1 полагаем что с=с, но в ходе опытов оказалось что скорость света одинакова отсюда следует, что t  не равен t1 т.к.  x не равен x1 А из того что время течет по разному события происходят в одной системе отсчета неявляется таковой в другой системе отсчета и что продольная система тела перемещается из одной ……..

Таким образом оказалось что время и пространство системы тел не является инвариантной. Преобразование Галилея не выполняется при релятивистских скоростях в релятивистской механике справедливым считать преобразованием Лоренца.

Правило сложение скоростей:

 

 

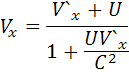
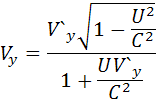
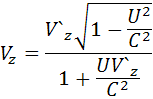
16) Релятивистские выражения: массы, импульса, энергий. Взаимосвязь массы и энергий. Инвариантность СТО.

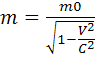 - релятивистское выражение массы,  m0- масса покоя тела

 - полная энергия движ. Тела.

 - полная энергия покоящегося тела.

 - релятивистский импульс

 - взаимосвязь импульса и энергий

- взаимосвязь массы и энергий.

Инвариантность СТО

Согласно 2-му постулату одной из инвариаций является скорость света, а время и размер является относительной.

Из СТО следует что пространство и время нельзя рассматривать отдельно независимо друг от друга они образуют единый 4-х мерный континиум и расстояние между 2-мя любыми точками этого 4-х мерного пространства время и является инвариантной 4-х мерной интерв. Задается при помощи времени подобных координат которая равна производной скорости света и времени c*t и расстоянию между 2-мя любыми точками определена как.